Now reprove the result of Exercise 51 using vector geometry. Assume that the cylinder has equation x² + y² = r² and the plane has equation z = ax + by.

Data From Exercise 51

Assume that the cylinder in Figure 15 has equation x² + y² = r² and the plane has equation z = ax + by. Find a vector parametrization r(t) of the curve of intersection using the trigonometric functions y = cos t and y = sin t.

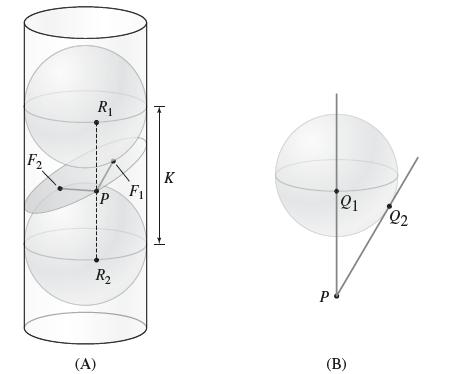
(a) Show that the upper and lower spheres in Figure 15 have centers C = (0,0,r Va + b + 1) C = (0,0,-r Va + b + 1) (b) Show that the points where the plane is tangent to the sphere are F = F2= :(a, b, a + b) a + b + 1 -r Va + b + 1 (a, b, a + b) Show that CF and CF2 have length r and are orthogonal to the plane. (c) Verify, with the aid of a computer algebra system, that Eq. (2) holds with K = 2r Va + b + 1 To simplify the algebra, observe that since a and b are arbitrary, it suffices to verify Eq. (2) for the point P = (r, 0,ar).