Potential Due to a Uniform Sphere Let \(\mathcal{S}\) be a hollow sphere of radius \(R\) with its center at the origin with a uniform mass distribution of total mass \(m\) [since \(\mathcal{S}\) has surface area \(4 \pi R^{2}\), the mass density is \(\left.\delta=m /\left(4 \pi R^{2}ight)ight]\). With \(G\) representing the universal gravitational constant, the gravitational potential \(V(P)\) due to \(\mathcal{S}\) at a point \(P=(a, b, c)\) is equal to
\[
-G \iint_{\mathcal{S}} \frac{\delta d S}{\sqrt{(x-a)^{2}+(y-b)^{2}+(z-c)^{2}}}
\]

(a) Use symmetry to conclude that the potential depends only on the distance \(r\) from \(P\) to the center of the sphere. Therefore, it suffices to compute \(V(P)\) for a point \(P=(0,0, r)\) on the \(z\)-axis (with \(r eq R\) ).
(b) Use spherical coordinates to show that \(V(0,0, r)\) is equal to
\[
\frac{-G m}{4 \pi} \int_{0}^{\pi} \int_{0}^{2 \pi} \frac{\sin \phi d \theta d \phi}{\sqrt{R^{2}+r^{2}-2 R r \cos \phi}}
\]
(c) Use the substitution \(u=R^{2}+r^{2}-2 R r \cos \phi\) to show that
\[
V(0,0, r)=\frac{-m G}{2 R r}(|R+r|-|R-r|)
\]
(d) Verify Eq. (12) for \(V\).

Transcribed Image Text:

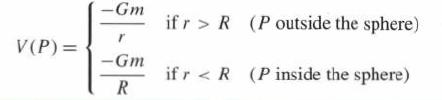
V(P) = -Gm r -Gm R ifr> R (P outside the sphere) if r < R (P inside the sphere)