Question: Prove that the length of a curve as computed using the arc length integral does not depend on its parametrization. More precisely, let C be

Prove that the length of a curve as computed using the arc length integral does not depend on its parametrization. More precisely, let C be the curve traced by r(t) for a ≤ t ≤ b. Let ƒ (s) be a differentiable function such that ƒ(s) > 0 and ƒ(c) = a and ƒ(d) = b. Then r₁(s) = r(ƒ(s)) parametrizes C for c ≤ s ≤ d. Verify that

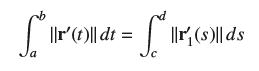
S ||r' (t)|| dt = ||r(s)|| ds

Step by Step Solution

★★★★★

3.36 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Hence By the Chain Rule we have rt tr pt S rt tr yt ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Let (A, R) be a poset in which the length of a longest (maximal) chain is n 2. Let M be the set of all maximal elements in (A, R), and let B = A - M. If R' = (B B) R, prove that the length of a...

On Dec. 1, 2014 Pete Fiore opened Flore Consulting Services, Inc. He provides marketing seminars guaranteed to increase sales by SK. The first fiscal (calendar) year will end December 31, 2014. One...

The Aggie Watch Corporation manufactures watches on a conveyor belt with 6 stations. One worker stands at each station and performs the following tasks: a . Where in the process is the bottleneck? b...

MA 261 PRACTICE PROBLEMS 1. If the line ` has symmetric equations y x1 z+2 2 = 3 = 7 , nd a vector equation for the line `0 that contains the point (2; 1; 3) and is parallel to `. A. ~ = (1 + 2t)~...

GUARDIAN 19. At an air show, a jet has a trajectory following the curve y = x2. ANDITSNUT daniAV SECTION 14.3 / Arc Length and Speed 765 If when the jet is at the point (1, 1), it has a speed of 500...

Exercise 1: Read both the introduction to the section and Example 1 (p. 969 - 971). Explain what the differential ds is substituted with in the computation of the line integral here. The subsection...

2. Find a parametrization of the curve formed by the intersection of the surfaces y" - z? = x - 2 and y'+ 2" =9 with z 2 0 in two different ways. (In both cases, specify the domain - the allowable...

Use Maple, Matlab, or Mathematica to Draw and visualize a curve in three-dimensions, compute the length of this curve from t = 0 to t = Tf inal, and animate a point moving along the curve, Find an...

Critically evaluate the statement. Lease classification can raise earnings management concerns. Your answer shall cover the following key points: How do capital leases and operating leases affect the...

Which of the following is not a method that auditors use to control their exposure to sampling risk during the examination? a. Determining an appropriate sample size. b. Performing the appropriate...

I wish the meeting was over.

In this chapter, we talk about empowering employees for success. After reviewing the chapter and this you make the call, if you were James Staker what would you have done differently to get Bonnie on...

If the solution to a system of two linear equations containing two unknowns is x = 3, y= -2, then the lines intersect at the point________.

If the lines that make up a system of two linear equations are coincident, then the system is________and the equations are________.

Verify that the values of the variables listed are solutions of the system of equations. S2x - y = 5 [5x + 2y = 8 x = 2, y = -1; (2, 1)

Hello, Please provide me the ans of J,K and L thank you. solve keon has asked meena about pricing..... Since Meena hasn't advertised very heavily (she currently pays $300 a month for advertising on...

A company reported a gross profit percentage of 25% with net sales of $347,800. What is the amount of cost of goods sold? Multiple Choice O $86,950 0 $108,688 0 $326,063 0 $260,850

language is python In this problem we will implement the Shortest Path Algorithm that we discussed in the class. You have to write Python program that implements the algorithm discussed in the class...