Question: Show that 3 3 determinants can be computed using the diagonal rule: Repeat the first two columns of the matrix and form the products

Show that 3 × 3 determinants can be computed using the diagonal rule: Repeat the first two columns of the matrix and form the products of the numbers along the six diagonals indicated. Then add the products for the diagonals that slant from left to right and subtract the products for the diagonals that slant from right to left.

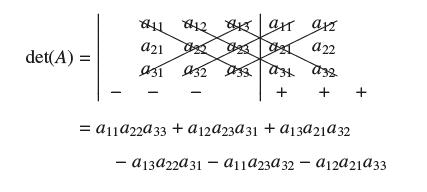
det(A) = a21 Ugg dg aga22 + = a11a22a33 + a12a23a31 + a13a21a32 - a 13a22a31 - a11a23a 32 - a12a21933

det(A) = a21 Ugg dg aga22 + = a11a22a33 + a12a23a31 + a13a21a32 - a13a22a 31 - a11a23a32a12a21933

Step by Step Solution

★★★★★

3.42 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Using the definition of 3 x 3 determinants given in Eq 2 we get 923 a23 de... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Write a literature review for your study. See below for an example of a literature review. Your literature review should provide both analysis and synthesis of previous studies as related to the...

The prototypes and diagrams that we have created have really given us a feel for the project, smiles Anna, looking up from her computer. I have a good sense about what we are doing. Same here,...

Adjustable-Rate and Subprime Mortgages The term subprime mortgage refers to mortgages given to home buyers with a heightened perceived risk of default, when, for instance, the price of the home being...

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

12:38 4 Assignment Details MTH 154-N41A: Quantitative Reasoning (SP21) MTH 154 Excel Project In this major project, you will create an Excel file and answer questions about linear and exponential...

Assume that you are preparing to confirm accounts receivable at December 31, 2022, which is one month prior to the fiscal year-end of January 31, 2023. The book value of gross accounts receivable is...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

What is Exercise 32-45? I don't quite understand it, so I'm not sure if my work or answers are correct. Linear Algebra Lab Exercises Linear algebra deals with vectors and linear functions that act on...

Jupyter NoteBook Once we decide to measure more than three features per input vector, it can become challenging to understand how a network is learning to solve such a problem since we can no longer...

The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 x 10" Pa and density of water is 10 kg/m.What fractional compression of water will be obtained at the bottom of the...

On December 31, Star Corp. had a reporting unit that had a book value of $ 950,000, including goodwill of $ 130,000. As part of the companys annual review of goodwill impairment, Star determined that...

In Exhibit 4, assume multiplex tickets cost $6 each, video rentals cost $2 each, and bags of popcorn cost $1 each. Suppose the consumer has $12 per week to spend on multiplex tickets, video rentals,...

How long does it take customers to pay the company? L01

The difference formula for the sine function sin(A - B) = ____.

If is an acute angle, solve the equation cos = 3/2.

The two triangles shown are similar. Find the missing length. 3 2.

(Capital structure theory) Match each of the following definitions to the appropriate terms: TERMS Independence theory-with corporate taxes Independence theory-no taxes Saucer-shaped cost-of-capital...

Kaye Blanchard is 50 years old. She has $54,000 of adjusted gross income and $12,800 of qualified medical expenses. She will be itemizing her tax deductions this year. How much of a tax deduction...

The code of a website has no impact on its accessibility. True False