Show that for k ≥ 1 and x ≠ 0,

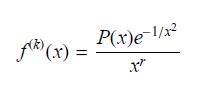
for some polynomial P(x) and some exponent r ≥ 1. Use the result of Exercise 71 to show that ƒ ^(k)(0) exists and is equal to zero for all k ≥ 1.

Data From Exercise 71

Let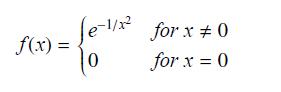

These exercises show that ƒ has an unusual property: All of its derivatives at x = 0 exist and are equal to zero.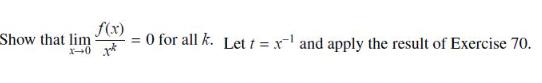

Data From Exercise 70

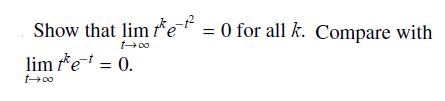
f(k)(x) = P(x)e-1/x X"