Question: Show that if (x) = px 2 + qx + r is a quadratic polynomial, then S 2 = b a (x) dx. In

Show that if ƒ(x) = px2 + qx + r is a quadratic polynomial, then S2 = ∫ba ƒ(x) dx. In other words, show that

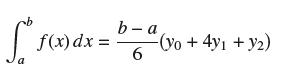
f f(x) dx =! b-a 6 -(yo+ 4y1 + y2)

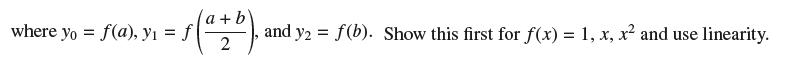
; (a+b) where yo = f(a), y = f and y2 = f(b). Show this first for f(x) = 1, x, x and use linearity.

So f f(x) dx = ! b-a 6 -(yo+ 4y1 + y2)

Step by Step Solution

★★★★★

3.34 Rating (148 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

this case For S Ax b a2 and the endpoints are a a b2 b Following the hint let fx 1 In S1 If ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

Show that if X is a continuous random variable, then where m is the median of X (see Exercise 2.17), EX ml, min E X - al E

Q:

Show that if X is a random variable having the Poisson distribution with the parameter and , then the moment-generating function of Z = X / That is, that of a standardized Poisson random...

Q:

Show that if X ~ X2 (v), then EX = v and Var (X) = 2v.

Q:

Please help answer the following four questions: Polynomials 7. Let Q(r) be a cubic polynomial and Q (1) = Q(2) = Q(4) = 0, Q(3) = 1. Determine Q(x). 8. (Optional) Let P(x) be a polynomial of degree...

Q:

Please generate answers to questions 13 and 21 in picture. Please show all work. thanks!! 274 CHAPTER 3 . Polynomial and Rational Functions 9-14 - Division of Polynomials Two polynomials P and D are...

Q:

This question concerns the portrayal of parse tree hubs for articulations made out of number constants, identififiers, and whole number administrators for expansion, deduction, increase and division....

Q:

For each of the following equivalences, state whether it holds or not, justifying each answer rigorously. (i) ((P ? Q) ? R) ? P ' P ? (Q ? R) [3 marks] (ii) (?x P(x)) ? (?x Q(x)) ' ?x [P(x) ? Q(x)]...

Q:

Adv Maths Question 36 I need correct answer otherwise compulsory I give multiple Dislikes Question 36 (i) The equation x 2 + bx + c = 0 has the property that if k is a root, then k 1 is a root. Show...

Q:

To be answered pls do it fast show solution i will rate helpful: ACTIVITY 1: In a convenient store, the number of teller (X) busy with customers at 12:00 noon varies from day to day. Past records...

Q:

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Q:

Using the data in BE25-6 and BE25-10, compute the overhead volume variance. Normal capacity was 25,000 direct labor hours.

Q:

Key issues involved in managing the components of IT infrastructureOutsourcing: Pros vs . ConsInfrastructure as a service ( IaaS ) cloud hostingSoftware as a Service ( SaaS ) PaaSVPNCRMSource...

Q:

12. What are Temporary Regulations? What weight do they carry in the tax researchers analysis?

Q:

Several mathematical stories originated with the second wedding of the mathematician and astronomer Johannes Kepler. Here is one: While shopping for wine for his wedding, Kepler noticed that the...

Q:

Make a complete graph of the following functions. If an interval is not specified, graph the function on its domain. Use a graphing utility to check your work. |f(x) = x + tan x on

Q:

a. Find the critical points of the following functions on the domain or on the given interval. b. Use a graphing utility to determine whether each critical point corresponds to a local maximum, local...

Q:

The methods of accounting for a lease by the lessee are: A. Operating and capital lease methods. B.Operating sales, and capital lease methods. C. Operating and finance lease methods. D. None of these...

Q:

13. In the following graph, all the edges have capacity equal to one. (a) For the given flow from s to t, draw the residual network. (b) Is it possible to increase the network flow (from 3 to 4)? Why...

Q:

Show me the Online Shooping Cart program in C++ that can use both inheritance and recursion techniques by deploying these concepts to the design by using additinal code. Include in the program,...