Question: Show that S 2 also gives the exact value for b a x 3 dx and conclude, as in Exercise 63, that S N
Show that S2 also gives the exact value for ∫ba x3 dx and conclude, as in Exercise 63, that SN is exact for all cubic polynomials. Show by counterexample that S2 is not exact for integrals of x4.
Data From Exercise 63
For N even, divide [a, b] into N subintervals of width Δx = b − a/N. Set xj = a + j Δx, yj = ƒ(xj), and
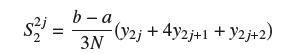
![(a) Show that Sy is the sum of the approximations on the intervals [X2, X2j+2]that is, Sy = S + S2 + ... +](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1701/7/8/9/490656f3f32bf6001701789490574.jpg)
Data From Exercise 62

s2= b-a 3N (V2j + 4y2j+1 + y2j+2)
Step by Step Solution
3.41 Rating (151 Votes )
There are 3 Steps involved in it
Data From Exercise 62 get Let fx x Then Ax b a2 and the endpoints are ... View full answer

Get step-by-step solutions from verified subject matter experts


