Question: Show that the power series (a)(c) have the same radius of convergence. Then show that (a) Diverges at both endpoints, (b) Converges at one endpoint

Show that the power series (a)–(c) have the same radius of convergence. Then show that (a) Diverges at both endpoints, (b) Converges at one endpoint but diverges at the other, and (c) Converges at both endpoints.

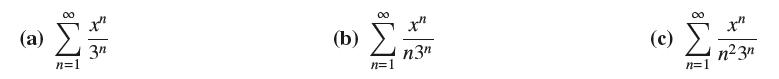
(a) M (b) T n3

(a) M (b) T n3" (c) & T 3

Step by Step Solution

★★★★★

3.43 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a With an 7 an1 p lim n0 an x1 3 lim lim n0 3n1 xn n0 3 Thus p ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

We show that the power series for the exponential function centered at 0 is Use the methods of this section to find the power series for the following functions. Give the interval of convergence for...

\fFind the interval of convergence of the power series. {He sure to include a check for convergence at the endpoints of the interval.) E\": (1}"n!{x 9)" rr= o 5\" Ox = 9 06 E x (-1 ) 2 X - V 2n! Need...

just let me know answers only. don't need to explain DEIA VERS Use the definition of Taylor series to find the Taylor series (centered at c) for the function. f ( x) = e4X, c=0 00 (4)n-1 f ( x ) = >...

1. In this question, we will see a technique commonly used in mathematics: comparison. We arcsin(x) da) in two different ways and compare the result. In compute the same quantity: general, this...

Identify the center of the following series, and then use the Ratio Test to find the radius of convergence. 2 n S o oeear n=1 Center a Radius R Find the center and radius of the interval of...

1. (60 pts True/False. Indicate whether the statement is true or false. If the statement is false, present an explanation or counterexample. (No explanation necessary for each true statement.) (2...

Section 10.7 Power Series Make sure you read the questions very carefully and see on what its being asked for. Please be very serious careful with this assignment. Feedback: #1: A similar issue is...

For reactions carried out under standard-state conditions, Equation (18.10) takes the form G = H - TS. (a) Assuming H and S are independent of temperature, derive the equation where K1 and K2 are the...

Listen to "Federal Court to Weigh Graphic Cigarette Labels Links to an external site." and provide an update on the status of the case as of today. (be sure to include your sources). this is the...

FASB 1 4 1 R ( ASC 8 0 5 ) requires that ongoing ( i . e . , in - process ) research and development projects acquired in a business combination be treated in all of the following ways except:...

How do company policies, such as compensation plans, influence salespeople? AppendixLO1

Differentiate. g(x) = (x + 2x)e x

The figure shows the graph of a function f. Suppose that Newtons method is used to approximate the root s of the equation f (x) = 0 with initial approximation x 1 = 6. (a) Draw the tangent lines that...

2. As an employee would you prefer joining a start-up that offers options as a form of payment? Or, would you rather join a large well-established company that offers options as a form of payment for...

1 6 : 4 5 Backend Programmin... 1 - University of Applied Sciences Europe Backend programming Final Exam Project Backend Programming: Project War Card Game Object Oriented Solution - With GUI 5 0...

Question 2 Who are the main users of financial statements? Explain what information these users will be interested in. TOTAL MARKS =15