Question: Suppose that Q(x) = (x a)(x b), where a b, and let P/Q be a proper rational function so that (a) Show

Suppose that Q(x) = (x − a)(x − b), where a ≠ b, and let P/Q be a proper rational function so that

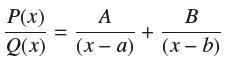
P(x) Q(x) A (x-a) + B (x-b)

(a) Show that 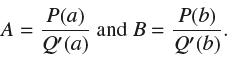A = P(a) Q'(a) and B= P(b) Q' (b)

(b) Use this result to find the partial fraction decomposition for P(x) = 3x − 2 and Q(x) = x2 − 4x − 12.

P(x) Q(x) A (x-a) + B (x-b)

Step by Step Solution

★★★★★

3.45 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Clearing denominators gives us Setting x a then yields while setting x b yields therefore ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

A first step to checking the ADA accessibility of your site may be to: Remove all small type from the site Purchase a site that claims to be ADA compliant Ask your website provider about current...

Q:

The process of adding rational functions (ratios of polynomials) by placing them over a common denominator is the analogue of adding rational numbers. The reverse process of taking a rational...

Q:

The process of adding rational functions (ratios of polynomials) by placing them over a common denominator is the analogue of adding rational numbers. The reverse process of taking a rational...

Q:

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Q:

Can you please answer the questions clearly ? 4 6 (a) Show that, for x # - 2. x42 =X-2. b) Are the functions f(x) and g(x) equal? Show that the function y = 19 can be written in the form y = ex....

Q:

---- ALL ANSWERS MUST BE WRITTEN IN EXCEL FORMULAS. A1 face TABLE 2 B D E F G H I J K L M N O P 0 1 TABLE 2 Present Value of $1 2 3 periods 1.00% 1.50% 2.00% 2.50% 3.00% 3.50% 4.00% 4.50% 5.00% 5.50%...

Q:

Next question Find the derivative of y with respect to x. y = In(10x) + 9x dy dxNext question Use logarithmic differentiation to find the derivative of y with respect to t. V11t y = t . . . dy its dt...

Q:

PART I: The Problem Statement The MoreBook company has decided to try publishing books as a way to make money for the company. A famous writer Daniel written a new book and she plans to sell an...

Q:

Please answer the following questions uploaded and please show all of the work. Thank you very much! 1. Help Q Q 1 2 | @ @ search Question 1 (24 Points) A bar in Tel Aviv offers its guests two types...

Q:

Please show me the work and show me the answer. Thank you. MATH 108 Problem Set 2: Section 2.4-2.7 Section 2.4: Dividing Polynomials; Factor/Remainder Theorem 1) Divide the following using long...

Q:

The company's assets under management (AUM) are $50 billion in total. The fund has an expense ratio of 0.5%. What is the total annual revenue of the fund originating from fees?

Q:

At what values of the ratio of the kinetic energy to rest energy can the velocity of a particle be calculated from the classical formula with the relative error less than = 0.010?

Q:

Describe and discuss the information you have found on each company with regard to its mission, vision, and value statements.

Q:

7 The National Cat Foundling Home encourages people to adopt its cats, but (because of limited funds) it allows each prospective owner to inspect only four cats before choosing one of them to take...

Q:

True or False Every polynomial function of degree 3 with real coefficients has exactly three real zeros.

Q:

If r is a real zero of even multiplicity of a function f, then the graph of f _______ (crosses/touches) the x-axis at r.

Q:

In problem, use the graph of the function f to solve the inequality. (a) f(x) > 0 (b) f(x) ¤ 0 3 y = 1 3 4 5 x -4 -3 -2 -2 x= 2 X=-1

Q:

Let x=0,y=0,z=0, and w=1. Evaluate each of the following Boolean expressions. 1. xyz+yw= 2. x(w+z)+zy= 3. (x+y)(w+z)= 4. x+(yz+zx)w= 5. (w+x+z)(y+w)(x+y+z)=

Q:

The Marchetti Soup Company entered into the following transactions during the month of June: (1) purchased inventory on account for $165,000 (assume Marchetti uses a perpetual inventory system); (2)...

Q:

Problem 12-3 After tax salvage value Karsted Air Services is now in the final year of a project. The equipment originally cost $32 million, of which 85% has been depreciated. Karsted can sell the...