The 1-Dimensional Brouwer Fixed Point Theorem. It indicates that every continuous function mapping the closed interval [0, 1] to itself must have a fixed

The 1-Dimensional Brouwer Fixed Point Theorem. It indicates that every continuous function ƒ mapping the closed interval [0, 1] to itself must have a fixed point; that is, a point c such that (c) = c.

Show that if ƒ is continuous and 0 ≤ ƒ (x) ≤ 1 for 0 ≤ x ≤ 1, then ƒ(c) = c for some c in [0, 1] (Figure 7).

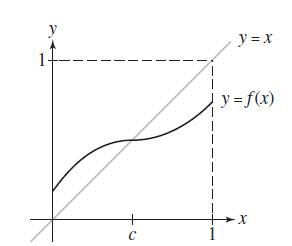
1 y y = x y = f(x) X