Question: The area function F(x) = x 0 1 t 2 dt is an antiderivative of (x) = 1 x 2 . Prove

The area function F(x) = ∫x 0 √1 − t2 dt is an antiderivative of ƒ(x) = √1 − x2. Prove the formula

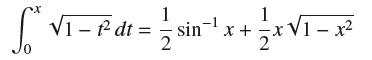
1 1 *VI-Pdt = sin x + x V - Vi 2 S 0

using geometry by interpreting the integral as the area of part of the unit circle.


1 1 *VI-Pdt = sin x + x V - Vi 2 S 0

Step by Step Solution

★★★★★

3.37 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The integral So 1 1 dt is the area bounded by the unit circle the ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

The graph of a function f is shown. Let t be the function that represents the area under the graph of f between 0 and x. (a) Use geometry to find a formula for g(x). (b) Verify that t is an...

Q:

The graph of a function f is shown. Let t be the function that represents the area under the graph of f between 0 and x. (a) Use geometry to find a formula for g(x). (b) Verify that t is an...

Q:

Use Theorem I to compute the shaded area in Exercise 7. Theorem I: Area under a Graph If f(x) is a continuous nonnegative function on the interval a x b, then the area under the graph of f(x),...

Q:

1. Compute integral Je-* dx using composite trapezoidal rule with 5 integration points. Estimate the integration error. (4 grading points) 3. Find the root of the equation e * - sin(x) cos (x) = 0...

Q:

1. [4 marks] Evaluate the following limits using calculus and showing all working. 3. [7 marks] (a) lim 2 + 2x - 3 (a) Sketch the graph of f (x) = VI. 2- 1 4x - 1-+ 30 (b) lim 1-+00 20(1 - 12) (b)...

Q:

1. [4 marks] Evaluate the following limits using calculus and showing all working. 3. [7 marks] (a) lim 2 + 2x - 3 (a) Sketch the graph of f (x) = VI. 2- 1 4x - 1-+ 30 (b) lim 1-+00 20(1 - 12) (b)...

Q:

Question: True or False. If it is false please note why the statement is false. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10] 11] 12] 13] 14] 15] 16] 17) 18] 19) 20] 21) 22] 23] 24) 25] 26] 27) 28] 29] 30] 31] 32]...

Q:

Written Assessment 1: Antiderivative of a Function Name: Date: I. Find the integral of the following. (5 pts each) 2w+1 2x + 9-2x 1. J (w+2)+(w-1)4 aw 2. J e2X - p-2x dx 3. (e +1)2 cos" z dz ey - dy...

Q:

9:54 20 0 Q & l 67% Total Points: 32 1. [4 pts] The image below depicts the function f (x) =0.2x with ten rectangle areas spanning the interval from x=1 to x=6 using right endpoints to calculate the...

Q:

Questions: please solve (ii) In the four-by-four version of the game, starting with pattern explain why it is impossible to reach a pattern with only one white counter. [Hint: don't try to write out...

Q:

Decide which of the following statements are true and which are false. Prove the true ones and provide counterexamples for the false ones. a) If f(x) as x and g(x) > 0, then g(x)/f(x) 0 as x ....

Q:

Draw the most stable conformation of 1, 4-dichiorobutane, using wedges and dashes to represent bonds coming out of the paper and going behind the paper, respectively.

Q:

If employee Zeke asks you to date the last paycheck that you hand out in 2 0 2 3 as " 2 0 2 4 , " you should: agree to defer the pay, but withhold FICA and FIT in 2 0 2 1 refuse to postdate the check...

Q:

Find the Present Value of `80,000 to be received after 10 years at the discount/interest rate of 12%.

Q:

Solve each inequality for x. (a) 1

Q:

Find an expression for the function whose graph is the given curve. 1

Q:

Find an expression for the function whose graph is the given curve. The top half of the circle x 2 + (y 2) 2 = 4

Q:

convert the following decimal numbers to 8 bit binary

Q:

You bought a share of Bavarian Sausage stock for $46.50 at the beginning of the year. During the year the stock paid $2.75 dividend and at the end of the year it trades at $52.75. What is the total...

Q:

4) In Matlab, generate a square matrix [A] of random numbers having n rows, for n = 100, 200, 500, 1000, 2000, 5000 and 10,000. (Don't display these!). Also generate a random column matrix (i.e., n...