The Laplace operator is defined by = xx + yy . A function (x, y) satisfying the Laplace equation = 0

The Laplace operator is defined by Δƒ = ƒ_xx + ƒ_yy. A function ƒ(x, y) satisfying the Laplace equation Δƒ = 0 is called harmonic. A function ƒ(x, y) is called radial if ƒ(x, y) = g(r), where r = √x² + y².

Use Eq. (12) to prove that in polar coordinates (r, θ),

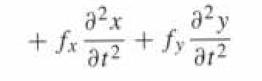
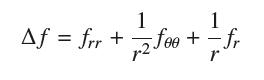
2x + fx a + fy a y ar