Question: The torus (doughnut-shaped solid) in Figure 15 is obtained by rotating the circle (x a) 2 + y 2 = b 2 around the

The torus (doughnut-shaped solid) in Figure 15 is obtained by rotating the circle (x − a)² + y²= b² around the y-axis (assume that a > b). Show that it has volume 2π2ab2. After simplifying it, evaluate the integral by interpreting it as the area of a circle.

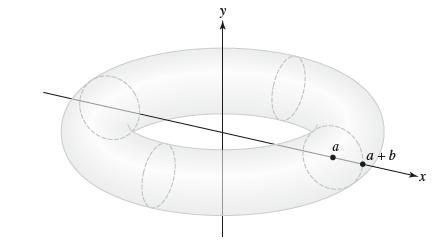
a a+b -X

Step by Step Solution

★★★★★

3.32 Rating (179 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Rotating the region enclosed by the circle x a y b about the yaxis produces ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Using Refactoring Miner to detect refactorings Description: The purpose of this assignment is to understand how to detect refactorings and design improvements, performed by developers as part of...

It is known that for a given area Iy = 300 in4 and Ixy = 125 in4, where the x and y axes are rectangular centroidal axes. If the axis corresponding to the maximum product of inertia is obtained by...

a. A torus of revolution (doughnut) is obtained by rotating a circle C in the xz-plane about the z-axis in space. If C has radius r > 0 and center (R, 0, 0), show that a parametrization of the torus...

Paoatnn 1 Consider the bridge truss diagrannued below: Given a vector of edema] forces [what we call the \"data\" or the \"right hand side"] b on the bridge. we can compute the forces F1. F2. . .. ....

Area of a Torus Let $\mathcal{T}$ be the torus obtained by rotating the circle in the $y z$-plane of radius $a$ centered at $(0, b, 0)$ about the $z$-axis (Figure 23). We assume that...

175 Homework B Section 6.3 (Part II) 1 of 3 https://www.webassign.net/web/Student/Assignment-Responses/last?dep... WebAssign 175 Homework B Section 6.3 (Part II) (Homework) Current Score : - / 5...

Example 1 Show that the volume of a sphere of radius r is V = Solution If we place the sphere so that its center is at the origin (see Figure 4), then the plane Pr intersects the sphere in a circle...

I know this is alot but I am behind I will greatly appreciate the help. Please show all your work and be neat as possible please. Example 4 The region 9 enclosed by the curves y = 2x and y = x is...

1: Find the volume of the solid obtained by rotating the region bounded by y = a" , y = 0, and = = 5, about the y-axis. V = 2: Find the exact value of the volume of the solid obtained by rotating the...

12. [-10.13 Points] DETAILS SCALCET9 6.2.029. OH 00 Submissions Used MY NOTES ASK YOUR TEACHER Three regions are dened in the figure. )1 C(o,2 o ' A(1,0) G) Find the volume generated by rotating the...

3. Which one of the following features is not present in female frog? A. webbed feet B. tympanum C. copulatory pad D. Fore limbs

Q: Solve the following integrals (4 * only): (each 25 marks) 1. [ 8e" dt 2. (1-3x)sin (x) dx 3. L wet" dw 4. [ (2x)' In (4x)dx 5. [(6+3:)cos(1+4:)dz

q , costs include anything a buyer must give up to obtain the benefits the product provides. Multiple Choice Overhead Customer Manufacturing Variable Promotional

Identify and evaluate examples of existing businesses in your country that would appear to match the four main product areas as likely partners.

Assuming that u1 = 0 and un+1 = 1.1un determine a convergent sequence, find limn( to four decimal places?

Show that {un} of Problem 41 is increasing and bounded above by 2?

Using the definition of limit, prove that limn( n / (n+1) = 1; that is, for a given ( > 0, find N such that n ( N | n / (n + 1) - 1 |

a.On July 1, 2020, a three-year insurance premium on equipment in the amount of $1,680 was paid and debited in full to Prepaid Insurance on that date. Coverage began on July 1

Regulations state that programs must have at least one person who holds a valid certificate in CPR and first aid on the premises of the program during program hours. a . true b . false

Some structured programming design techniques: [ A ] Your S 1 ( for Game 1 ) may be defined as follows: CS 1 1 9 Python Programming Project 1 1 ( PJ 1 1 ) Dr . Lin Version 3 / 1 / 2 4 Page 3 of 5 #...