This exercise shows that the multiplier may be interpreted as a rate of change in general. Assume that the maximum of (x, y) subject

This exercise shows that the multiplier λ may be interpreted as a rate of change in general. Assume that the maximum of ƒ(x, y) subject to g(x, y) = c occurs at a point P. Then P depends on the value of c, so we may write P = (x(c), y(c)) and we have g(x(c), y(c)) = c.

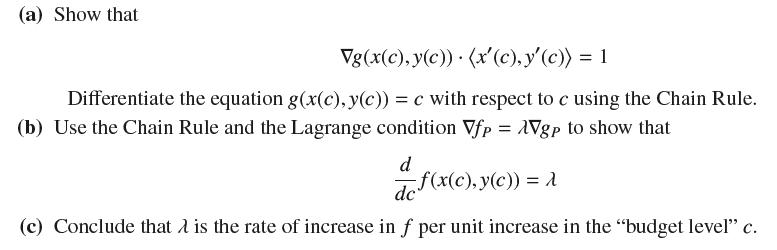
(a) Show that Vg(x(c), y(c)) (x'(c), y'(c)) = 1 Differentiate the equation g(x(c), y(c)) = c with respect to c using the Chain Rule. (b) Use the Chain Rule and the Lagrange condition Vfp = AVgp to show that d de f(x(c), y(c)) = A dc (c) Conclude that is the rate of increase in f per unit increase in the "budget level" c.