This is a continuation of Exercise 76. Data From Exercise 76 Set Im = /2 0 sin m x dx. Use Exercise 69 to

This is a continuation of Exercise 76.

Data From Exercise 76

Set Im = ∫^π/2₀ sin^m x dx. Use Exercise 69 to prove that

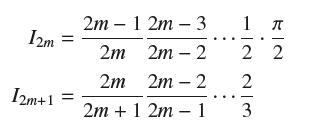
Conclude that

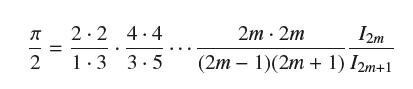
Data From Exercise 69

Let I_m = ∫^π/2₀ sin^m x dx.

Show that I₀ = π/2 and I₁ = 1.
Prove that, for m ≥ 2,

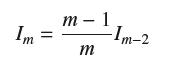
(a) Prove that I2m+1 12m 12m-1. sin2m+1 12m-1 12m+1 (c) Show that 1 (b) Show that = 1 + (d) Prove that lim m-0 1 2m 1+ 12m 12m+1 12m 12m+1 (e) Finally, deduce the infinite product for discovered by English mathematician John Wallis (1616-1703): = 1. 1 2m KIN x sin2m x sin2m-1. X for 0x 1/ 2244 3 3 5 = lim 2 m-00 1 2m. 2m (2m 1)(2m + 1)