Three towns A, B, and C are to be joined by an underground fiber cable as illustrated
Question:
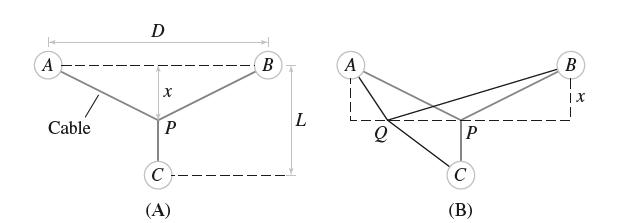
Three towns A, B, and C are to be joined by an underground fiber cable as illustrated in Figure 39(A). Assume that C is located directly below the midpoint of AB. Find the junction point P that minimizes the total amount of cable used.
(a) First show that P must lie directly above C. Use the result of Example 7 to show that if the junction is placed at point Q in Figure 39(B), then we can reduce the cable length by moving Q horizontally over to the point P lying above C.
(b) With x as in Figure 39(A), let ƒ(x) be the total length of cable used. Show that ƒ has a unique critical point c. Compute c and show that 0 ≤ c ≤ L if and only if D ≤ 2 √3 L.
(c) Find the minimum of ƒ on [0, L] in two cases: D = 2, L = 4 and D = 8, L = 2.
Example 7
Step by Step Answer:
a Look at diagram 39B Let T be the point directly above Q on AB Let s AT and D AB so that TB Ds Let ...View the full answer
