Use Theorem 2 to prove that the (x) is represented by its Maclaurin series for all x. Using Maclaurin series, determine to exactly what value

Use Theorem 2 to prove that the ƒ(x) is represented by its Maclaurin series for all x.

Using Maclaurin series, determine to exactly what value the following series converges:

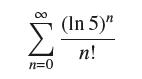
THEOREM 2 Let I = (c-R,c + R), where R > 0, and assume that f is infinitely differentiable on 1. Suppose there exists K> 0 such that all derivatives of f are bounded by K on I: |f(k)(x)| K Then f is represented by its Taylor series in 1: f(x) = n=0 for all k20 and x = 1 f(n)(c). n! -(x - c)" for all x I