Verify Eq. (11) for the functions in Exercise 44. Data From Exercise 44 A function (x, y, z) is called homogeneous of degree n if

Verify Eq. (11) for the functions in Exercise 44.

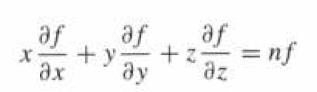
Data From Exercise 44

A function ƒ(x, y, z) is called homogeneous of degree n if ƒ(λx, λy, λz) = λn ƒ(x, y, z) for all λ ∈ R.

Show that the following functions are homogeneous and determine their degree:

af af X +2 =nf z af ax