Verify that function F(x) = x tan 1 x 1/2 ln(x 2 + 1) is an antiderivative of (x) = tan 1 x satisfying

Verify that function F(x) = x tan⁻¹ x − 1/2 ln(x² + 1) is an antiderivative of ƒ(x) = tan⁻¹ x satisfying F(0) = 0. Then use the result of Exercise 53 with x = √1/3 to show that

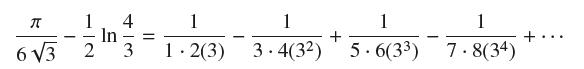
Use a calculator to compare the value of the left-hand side with the partial sum S₄ of the series on the right.

1 4 In 63 2 3 - - = 1 1.2(3) 1 3.4(32) + 1 5.6(3) 1 7.8(34) +.