Question: Verify that T n (x) = 1 + x + x 2 + + x n is the nth Maclaurin polynomial of

Verify that T_n(x) = 1 + x + x² + · · · + xⁿ is the nth Maclaurin polynomial of ƒ(x) = 1/(1 − x). Show using substitution that the nth Maclaurin polynomial for ƒ(x) = 1/(1 − x/4) is

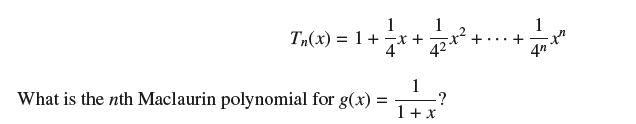
Tn(x) =1 + ax + What is the nth Maclaurin polynomial for g(x) = = 1 1 1 + x ? +...+ 1 pr 4n

Step by Step Solution

★★★★★

3.33 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let fx 1x Then fx 1x fx 21x fx 31 x4 and in general fnx n1xn1 Ther... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

In Exercises determine whether (x) approaches or - as x approaches 4 from the left and from the right. f(x) = = 1 x 4

Find constants A and B such that the equation is true. 23 - x 2x + 7x - 4 2x - 1 B x + 4

In Problem perform the indicated operations and simplify. 1 x - 2 x - 2 4

In this problem, you will use a linear approximation to approximate V493. Let an) = E The linear approximation of f(C) at w = 49 can be written in the form L(:L') = ma: + b' Compute m and b. c l |...

You are given the coefficients \ alpha 0 , \ alpha 1 , . . . , \ alpha n of a polynomial P ( x ) = Xn k = 0 \ alpha kx k = \ alpha 0 + \ alpha 1 x + \ alpha 2 x 2 + + \ alpha nx n , and you want to...

You are given the coefficients \ alpha 0 , \ alpha 1 , . . . , \ alpha n of a polynomial P ( x ) = Xn k = 0 \ alpha kxk = \ alpha 0 + \ alpha 1 x + \ alpha 2 x 2 + + \ alpha nx n , and you want to...

You are given the coefficients \ alpha 0 , \ alpha 1 , . . . , \ alpha n of a polynomial P ( x ) = Xn k = 0 \ alpha kxk = \ alpha 0 + \ alpha 1 x + \ alpha 2 x 2 + + \ alpha nxn , and you want to...

The notes that the teacher gave are beyond confusing. HELP PLEASE 9. Determine the remainder when P(x) = 2x3 - 12x + 4 is divided by x + 4 using: a. Long Division (3) b. Synthetic Division (3) c. The...

Practice question SAMPLE/EXAMPLE: UV .. ONE WAY ANOVA TEST TWO College readiness Does the Rate of Poverty in a School Influence Keystone Math Scores? Use the attached table to get your data. Data...

If the odds of the Yankees beating the Red Sox are 5 to 3, what is the probability of this event happening?a.5/8 b.3/8 c.3/5 d.1/8 e.5/3

Santa Maria Village received voter approval to issue bonds for construction of a bike path, Including restrooms and picnic sheiters, along village oceanfront. The finance department has discussed...

9.42 An experiment reported in Popular Science compared fuel economies for two types of similarly equipped diesel mini-trucks. Let us suppose that 12 Volkswagen and 10 Toyota trucks were tested in...

6.7 Modify the snapshot algorithm to record the channel states as well as the processor states. Prove that your algorithm is correct.

Find a function whose graph is given. 2 4 6 8 10 x -4 -2

Use a calculator to approximate sin /8 Round the answer to two decimal places.

Use a calculator to approximate sec 10. Round the answer to two decimal places.

How marketing approach for Alibaba in China differs from the one in India and Germany?

The following selected transactions relate to liabilities of United Insulation Corporation. United

The Linux operating system is widely used in industry, especially for servers. Why do you believe this is the case?