We estimate integrals using Taylor polynomials. Exercise 72 is used to estimate the error. (a) Compute the sixth Maclaurin polynomial T 6 for (x) =

We estimate integrals using Taylor polynomials. Exercise 72 is used to estimate the error.

(a) Compute the sixth Maclaurin polynomial T₆ for ƒ(x) = sin(x²) by substituting x² in P(x) = x − x³/6, the third Maclaurin polynomial for ƒ(x) = sin x.

(b) Show that | sin(x²) − T₆(x)| ≤|x|¹⁰/5!. Substitute x² for x in the Error Bound for |sin x − P(x)|, noting that P is also the fourth Maclaurin polynomial for ƒ(x) = sin x.

(c) Use T₆ to approximate ∫₀^1/2 sin(x²) dx and find a bound for the error.

Data From Exercise 72

We estimate integrals using Taylor polynomials. 

Let L > 0. Show that if two functions ƒ and g satisfy |ƒ(x) − g(x)|

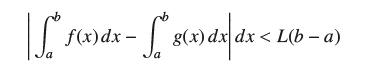
L'o f(x) dx - * 8(x) dx[\dx < L(b-a