Question: We explore functions whose graphs approach a nonhorizontal line as x . A line y = ax + b is called a slant asymptote

We explore functions whose graphs approach a nonhorizontal line as x → ∞. A line y = ax + b is called a slant asymptote if

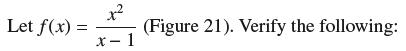
or lim (f(x) (ax+b)) = 0 X-00 lim (f(x) (ax + b)) = 0 X--0

Let f(x) = x x-1 (Figure 21). Verify the following:

(a) f(0) is a local max and f(2) a local min. (b) fis concave down on (-, 1) and concave up on (1, 0). (c)


or lim (f(x) (ax+b)) = 0 X-00 lim (f(x) (ax + b)) = 0 X--0

Step by Step Solution

★★★★★

3.37 Rating (147 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

2 Let fx 1 x1 xx 2 x 1 x 1 a Critical points of fx occur at x 0 and x 2x ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

Q:

We explore functions whose graphs approach a nonhorizontal line as x . A line y = ax + b is called a slant asymptote if Sketch the graph of Proceed as in the previous exercise to find the slant...

Q:

We explore functions whose graphs approach a nonhorizontal line as x . A line y = ax + b is called a slant asymptote if Show that y = 3x is a slant asymptote for (x) = 3x + x 2 . Determine whether...

Q:

We explore functions whose graphs approach a nonhorizontal line as x . A line y = ax + b is called a slant asymptote if If (x) = P(x)/Q(x), where P and Q are polynomials of degrees m + 1 and m, then...

Q:

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Q:

An open box is made from a square piece of cardboard 12 inches on a side by cutting identical squares from the corners and turning up the sides. Use this information to complete parts a through c. a....

Q:

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Q:

8 Rational Equations Algebra Review Express each sum as a single fraction by finding the least common denominator. 1. 3 I 2. 3. 1 3 I+1 - +5 2 4 z - 9 4. I+3 x2 + 8x + 15 22Practice: Identifying...

Q:

M05_CONS8612_04_SE_C05_01.qxd 10/8/10 11:10 PM Page 501 Activity 5.3 Activity 5.3 Percent Markup Objectives 1. Determine the domain of a rational function defined by an equation of the form k y = ,...

Q:

Hello, I need help working through my math 055 course activity, that is due 4/12/2017. Help would be appreciated! Percent Markup Objectives 1. Determine the domain of a rational function defined by...

Q:

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Q:

Jack Kelly Company has grown rapidly since its founding in 2002. To instill loyalty in its employees, Kelly is contemplating establishment of a defined benefit plan. Kelly knows that lenders and...

Q:

1. For cach of the following situations, decide whether Al has diminishing marginal utility. Explain. a. The more economics classes Al takes, the more he enjoys the subject. And the more classes he...

Q:

Interconnection Networks Consider a 4 \ times 4 Hypercube network, as shown in Figure 1 below. The dimensions of this 4 \ times 4 hypercube are depicted in the figure. Utilizing the tag routing...

Q:

A firm that produces mixes for cakes, cookies, and other baked items has an incoming toll-free line for customer service calls. The manager of the customer service reps has decided to base about a...

Q:

A 20 kg child is 3 m to the right of center. An 80 kg adult wishes to balance the see saw by sitting a distance x to the left of center. They will balance if the center of mass is exactly 0. Solve...

Q:

Experiment d. For the data presented in Section 6.6, Exercises 1-4, write the results in terms of a random variable and find the expectation. What fraction of experiments have a result less than the...

Q:

A 20 kg child is 3 m to the right of center, her 30 kg older brother is 1 m to the right of center, and an 80-kg adult wishes to balance the see saw by sitting a distance x to the left of center....

Q:

Explain the (a) lower of cost or net realizable value (LCNRV) approach and the (b) lower of cost or market (LCM) approach to valuing inventory. please answer in your own words, do not use the outside...

Q:

Can someone help me with this problem it is urgent I would really appreciate it x=7 TI . Na min

Q:

Standard Setters, such as the FASB, adopt a decision usefulness approach that often can result in a tradeoff between relevance and reliability. Briefly discuss your understanding this tradeoff and...