We will show that continuously compounded interest is a limiting case, as n → ∞, of periodically compounded interest. We first establish an important limit.
(a) Show that ln(1 + r) is the area under the graph of y = 1/x from 1 to 1 + r.
(b) Using rectangles with base length r, prove that

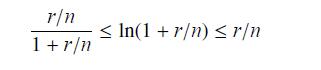
(c) Prove that

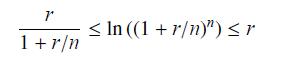
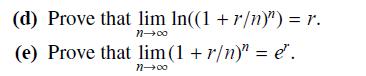
(f) Prove that for an interest rate r, continuous compounding of interest is the limit as n → ∞of n-times annual periodic compounding of interest.

r/n 1 +r/n < ln(1 + r/n) r/n