We wish to define the average value Av ( f ) Av ( f ) of a continuous function f f along a curve

We wish to define the average value $\mathrm{Av}\left(f\right)$ of a continuous function $f$ along a curve $C$ of length $L$. Divide $C$ into $N$ consecutive arcs $C_1,\dots ,C_N$, each of length $L/N$, and let $P_i$ be a sample point in $C_i$ (Figure 26). The sum

$$\frac{1}{N}\sum _{i=1}f\left(P_i\right)$$
may be considered an approximation to $\mathrm{Av}\left(f\right)$, so we define
$$\mathrm{Av}\left(f\right)=\underset{N\to \infty }{lim}\frac{1}{N}\sum _{i=1}f\left(P_i\right)$$
Prove that
$$\mathrm{Av}\left(f\right)=\frac{1}{L}{\int }_{C}f(x,y,z)ds$$
Show that $\frac{L}{N}{\sum }_{i=1}f\left(P_i\right)$ is a Riemann sum approximation to the line integral of $f$ along $C$.

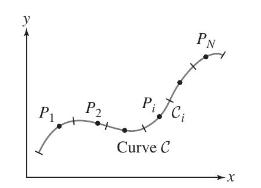
P2 Pi Ci Curve C PN X