When a spring with natural frequency /2 is driven with a sinusoidal force sin(t) with , it oscillates according to Let (a) Use

When a spring with natural frequency λ/2π is driven with a sinusoidal force sin(ωt) with ω ≠ λ, it oscillates according to

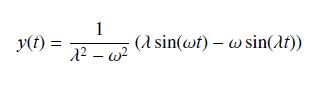
Let 

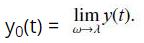
(a) Use L’Hôpital’s Rule to determine y₀(t).
(b) Show that y₀(t) ceases to be periodic and that its amplitude |y₀(t)| tends to ∞ as t → ∞(the system is said to be in resonance; eventually, the spring is stretched beyond its structural tolerance).

(c) Plot y for λ = 1 and ω = 0.8, 0.9, 0.99, and 0.999. Do the graphs confirm your conclusion in (b)?

y(t) = 1 1 - w (A sin(wt) - w sin(at))