Use Stokes Theorem to evaluate ∫∫_S curl F · ds.

F(x, y, z) = x²y³zi + sin(xyz)j + xyz k, S is the part of the cone y² = x² + z² that lies between the planes y = 0 and y = 3, oriented in the direction of the positive y-axis

Data from Stokes Theorem

Let S be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve C with positive orientation. Let F be a vector field whose components have continuous partial derivatives on an open region in R³ that contains S. Then

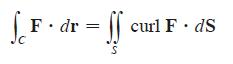
S F dr = ff S curl F. ds