(a) We found that f_x(1, 1) = −2 for the function f(x, y) = 4 − x² − 2y². We interpreted this result geometrically as the slope of the tangent line to the curve C₁ at the point P(1, 1, 1), where C₁ is the trace of the graph of f in the plane y = 1 . (See the figure.) Verify this interpretation by finding a vector equation for C₁, computing the tangent vector to C₁ at P, and then finding the slope of the tangent line to C₁ at P in the plane y = 1 .

(b) Use a similar method to verify that f_y(1, 1) = −4.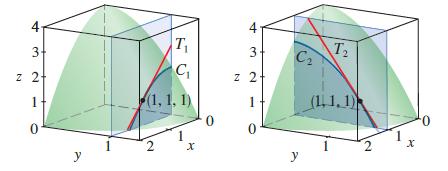

41 T T2 C2 3. z 21 z 21 (1, 1, 1) (111, 1) 1 1 1 y y 4, 3.