Question: Consider the angle u in standard position in a unit circle, where 0 < /2 or - /2 < < 0 (use
Consider the angle u in standard position in a unit circle, where 0 ≤ θ < π/2 or - π/2 < θ < 0 (use both figures).
a. Show that |AC| = |sin θ|, for -π/2 < θ < π/2.
b. Show that |sin θ| < |θ|, for -π/2 < θ < π/2.
c. Conclude that - |θ| ≤ sin θ ≤ |θ|, for -π/2 < θ < π/2.
d. Show that 0 ≤ 1 - cos θ ≤ |θ|, for -π/2 < θ < π/2.
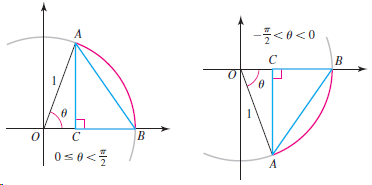
-
Step by Step Solution
3.47 Rating (160 Votes )
There are 3 Steps involved in it
a Suppose 0 2 Note that sin 0 so sin sin Also sin AC1 so AC sin Now suppose that 2 ... View full answer

Get step-by-step solutions from verified subject matter experts


