Consider the functions 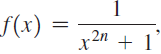where n is a positive integer.

a. Show that these functions are even.

b. Show that the graphs of these functions intersect at the points (±1, 1/2), for all positive values of n.

c. Show that the inflection points of these functions occur at 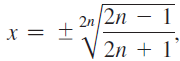for all positive values of n.

d. Use a graphing utility to verify your conclusions.

e. Describe how the inflection points and the shape of the graphs change as n increases.

F(x) .2n r2n + 1 2n 2n + V 2n + 1