Consider the quartic (fourth-degree) polynomial f(x) = x⁴ + bx² + d consisting only of even-powered terms.

a. Show that the graph of f is symmetric about the y-axis.

b. Show that if b ≥ 0, then f has one critical point and no inflection points.

c. Show that if b < 0, then f has three critical points and two inflection points. Find the critical points and inflection points, and show that they alternate along the x-axis. Explain why one critical point is always x = 0.

d. Prove that the number of distinct real roots of f depends on the values of the coefficients b and d, as shown in the figure. The curve that divides the plane is the parabola d = b²/4.

e. Find the number of real roots when b = 0 or d = 0 or d = b²/4.

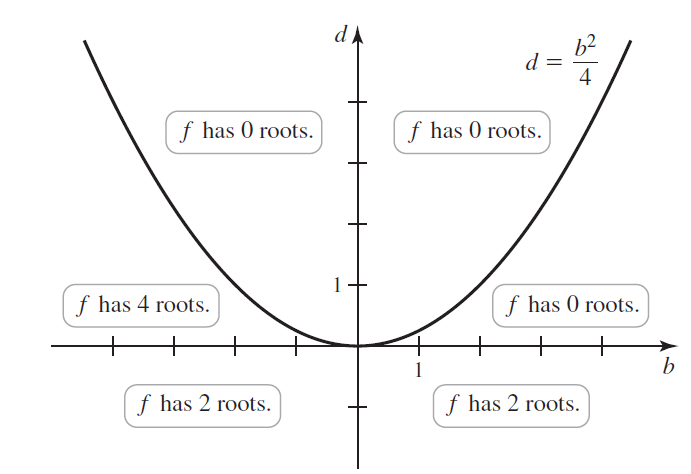
b2 f has 0 roots. f has 0 roots. f has 4 roots. f has 0 roots. + f has 2 roots. f has 2 roots.