Question: Given the function f(x) = 1 - cos x and the points A(/2, f(/2)), B(/2 + 0.05, f(/2 + 0.05)), C(/2 + 0.5, f(/2 +

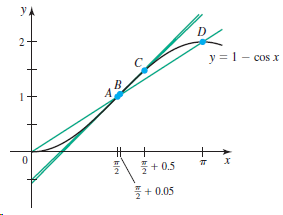
Given the function f(x) = 1 - cos x and the points A(π/2, f(π/2)), B(π/2 + 0.05, f(π/2 + 0.05)), C(π/2 + 0.5, f(π/2 + 0.5)), and D(p, f(p)) (see figure), find the slopes of the secant lines through A and D, A and C, and A and B. Then use your calculations to make a conjecture about the slope of the line tangent to the graph of f at x = π/2.

УА 2- y = 1- cos x 4. A + 0.5 + 0.05 elea

2- y = 1- cos x 4. A + 0.5 + 0.05 elea

Step by Step Solution

★★★★★

3.50 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

For line AD we have For line AC we have F... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

Given the function f (x) = (x - 5), use composition of functions to show that f -1(x) = x2 + 5.

Given the function f, prove that f is one-to-one using the definition of a one-to-one function. a. f (x) = 1/3 x - 6 b. f (x) = 4 - 2x c. f (x) = x3 + 1/2

Graph the function f (x) = cos x + 1/50 sin 50x using the windows given by the following ranges of x and y. (a) -5 x 5, - 1 y 1 (b) - 1 x 1, 0.5 y 1.5 (c) - 0.1 x 0.1, 0.9 y 1.1

Provide solutions.to the following questions. There are two types of individuals: high ability (type H) and low ability (type L). Regardless of their level of education, the lifetime productivity of...

Use a graph of f to estimate lim f(x) or to show that the limit does not exist. Evaluate f(x) near x = a to support your conjecture. X- a f ( x ) = 1- cos (5x - 5) 5 ( x - 1 ) 2 i a =1 Use a graphing...

with detailed solution 1. (28 points) CURVE SKETCHING. Given the function f (x) = x4 - 2x2 - 4 1. (2 points) Find f (x) and f"(x). 2. (16 points) Determine the following properties of the graph of f....

1. Find the domain of the function f ( x )= x 2 x +2 1) ______ (A) D=( ,2 ) ( 2, ) (B) D=( ,2 ) (2, ) (C) D= ( 2, ) (D) D=(2, ) (E) none of the above 1 2. According to the Center for Disease Control...

cck3 java help them all If a processor exhibited one branch delay slot how would you reorder (and possibly modify) the instructions in the following loop to gain a performance advantage? loop ldr...

What is a branch delay slot and why does it arise? [7 marks] How can branch delays be avoided? If a processor exhibited one branch delay slot how would you reorder (and possibly modify) the...

Fx(a, b, c)(x 15.5 EXERCISES Preliminary Questions 1. Which of the following is a possible value of the gradient Vf of a 4. function f(x. y) of two variables? po W (a) 5 (b) (3,4) (c) (3, 4. 5) 2....

The following forecasts of earnings per share (EPS) and dividend per share (DPS) were made at the end of 2009: The firm has an equity cost of capital of 12 percent per annum. (This is the same pro...

Warner Company manufactures and sells pottery items. All manufacturing takes place in one plant, having four departments, each department producing only one product. The four products are plaques,...

5.111 GSS: OR Select someone at random from the 1858 people in the table given in Exercise 5.107. What is the probability that the person is a Democrat OR a Republican?

Explain how Emirates marketing strategy has been successful in creating a positive brand image with current and potential customers. On October 25, 1985, Emirates flew its first routes out of Dubai...

Find the derivative. Simplify where possible. y = sinh -1 (tan x)

Find the limit. lim x0 sin x/sin x

If x 2 + xy + y 3 = 1, find the value of y''' at the point where x = 1.

Darling Corporation is evaluating a proposed capital budgeting project that will require an in in $112,000. The project in generate the following net cash flows: Assume the desired rate of return on...

A study examined the whether acute nicotine use impacts working memory in people who smoke every day. Working memory was assessed by recording the maximum amount of numbers a person can correctly...

Please choose one answer and explain briefly. The relationship of forwards and futures is best represented by the following statement(s) (a) If futures price movements and interest rate movements are...