Question: Let f be a nonnegative function with a continuous first derivative on [a, b] and suppose that g(x) = cf(x) and h(x) = f(cx), where

Let f be a nonnegative function with a continuous first derivative on [a, b] and suppose that g(x) = cf(x) and h(x) = f(cx), where c > 0. When the curve y = f(x) on [a, b] is revolved about the x-axis, the area of the resulting surface is A. Evaluate the following integrals in terms of A and c.

a.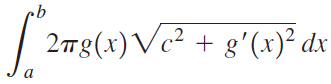 Г | 2тg(») Ve + 8 ()? dn a

b.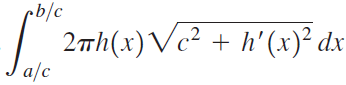 rb/c || + h'(x)² dx 2th(x)Vc² a/c

| 2g() Ve + 8 ()? dn a rb/c || + h'(x) dx 2th(x)Vc a/c

Step by Step Solution

★★★★★

3.51 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Note that gx cfx so that gx cfx 2 fogx c gx dx 2... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

Suppose f is a nonnegative function with a continuous first derivative on [a, b]. Let L equal the length of the graph of f on [a, b] and let S be the area of the surface generated by revolving the...

Let f be a nonnegative continuous function on [0,1]. (a) Show that (b) Use part (a) to evaluate xf(sin x) dx = (n/2) | f(sin x) dx. x sin x cos x ax.

Let f be a nonnegative continuous function defined on 0 ( x Show that (a) If limx( f(x) exists it must be 0; (b) It is possible that limx( f(x) does not exist. Roa f(x) dx

Assume f is a nonnegative function with a continuous first derivative on a b The curve y f x on a b is revolved about the x axis Explain how to find the area of the surface that is gen What is the...

MATH 115 Precalculus Fall, 2016, V1.1 MATH 115 FINAL EXAMINATION This is an open-book exam. You may refer to your text and other course materials as you work on the exam, and you may use a...

10 questions to be answered Given the function g(x) = 6x + 81x2 + 360x, find the first derivative, g'(x). g' (x) = Notice that g' (x) = 0 when x - - 5, that is, g'( - 5) = 0. Now, we want to know...

MATH 107 QUIZ 5 NAME: _______________________________ Instructor: J. Alexander I have completed this assignment myself, working independently and not consulting anyone except the instructor....

MATH 107 QUIZ 5 NAME: _______________________________ I have completed this assignment myself, working independently and not consulting anyone except the instructor. INSTRUCTIONS The quiz is worth...

Let f be an increasing function with F(0)= 3. The derivative of f is given by f'(x ) = cos ( Tix) + x + 6 ( a ) find f ( 3 ) ( b) Write an equation for the line tangent to the graph of y= (F(x ) at X...

Let f be a differentiable function and f (x) Let f be a differentiable function and f (X)

List and contrast several challenges of operating in the digital world.

1. What are the three key elements you need to consider when developing the definition of asset for your organization? a. Non-consumable, acquisition cost, and useful life b. Manufacturing year,...

The ELSE statement can be used on its own or in combination with an IF statement.

Before you see whether the prize is behind door 2, host Monty Hall opens a door that has no prize behind it. To be specific, suppose that before door 2 is opened, Monty reveals that there is no prize...

Test the series for convergence or divergence. (1)"+1 ne 3 + 4

Find the radius of convergence and interval of convergence of the power series. 00 n=1 x" 2n - 1

Determine whether the series is convergent or divergent. 00 *in* +1 3

is a benefit of borrowing. a. Providing payments that fit into a budget b. Having a permanent record of transactions c. The ability to buy expensive goods while spreading the payments over time d....

Question 1 (1 point) Assets such as this operate outside of central banking systems and use cryptography and control to create and secure financial transactions and verify the transfer of assets. a)...

Your client has two children. The younger one just turned 2, and the older one just turned 4. They are expected to go to college when they turn 18. College expenses are expected to be $25,000 per...