Let f(x) ax 2 bx c be an arbitrary quadratic function and choose two points x p and x q Let L 1 be the line tangent to the graph of f at the point (p, f(p)) and let L 2 be the line tangent to the graph at the point (q, f (q)) Let x s be the vertical line through the intersection point of L 1 and L ...

The equation of L is y 2ap bx p fp which can be written y 2apbx ap c The equation of L2 ...

Let f(x) = ax 2 + bx + c be an arbitrary quadratic function and choose two

Question:

Let f(x) = ax² + bx + c be an arbitrary quadratic function and choose two points x = p and x = q. Let L₁ be the line tangent to the graph of f at the point (p, f(p)) and let L₂ be the line tangent to the graph at the point (q, f (q)). Let x = s be the vertical line through the intersection point of L₁ and L₂. Finally, let R₁ be the region bounded by y = f(x), L₁, and the vertical line x = s, and let R₂ be the region bounded by y = f(x), L₂, and the vertical line x = s. Prove that the area of R₁ equals the area of R₂.

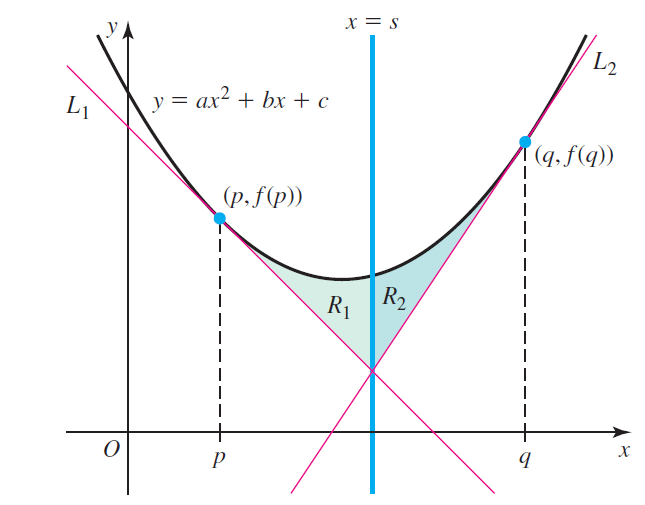
L2 y = ax? + bx + c L1 (q.f(q)) (p.f(p)) R2 R1