The expression

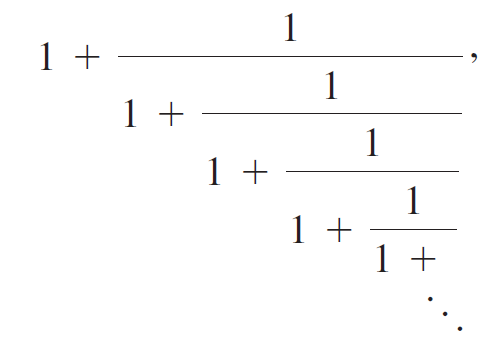
where the process continues indefinitely, is called a continued fraction.

a. Show that this expression can be built in steps using the recurrence relation a₀ = 1, a_{n + 1} = 1 + 1/a_n , for n = 0, 1, 2, 3, ?. . . Explain why the value of the expression can be interpreted asprovided the limit exists.

b. Evaluate the first five terms of the sequence {a_n}.

c. Using computation and/or graphing, estimate the limit of the sequence.

d. Assuming the limit exists, use the method of Example 5 to determine the limit exactly. Compare your estimate with (1 + ?5)/2, a number known as the golden mean.

e. Assuming the limit exists, use the same ideas to determine the value of

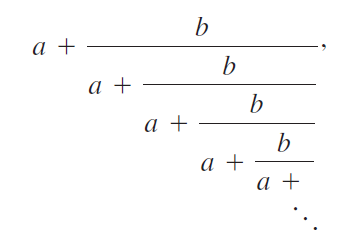
where a and b are positive real numbers.

1 + 1 + 1 + 1 1 1 + 1 1 1 + lim an n a + a + a + b b + D b b + D