The Fibonacci sequence {1, 1, 2, 3, 5, 8, 13, . . .} is generated by the recurrence relation

f_{n + 1} = f_n + f_{n - 1}, for n = 1, 2, 3,  . . , where f₀ = 1, f₁ = 1.

a. It can be shown that the sequence of ratios of successive terms of the sequence 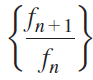has a limit φ. Divide both sides of the recurrence relation by f_n, take the limit as n→∞, and show that

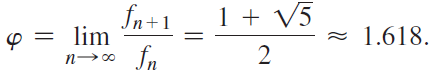
b. Show that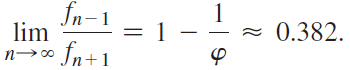

c. Now consider the harmonic series and group terms as follows:

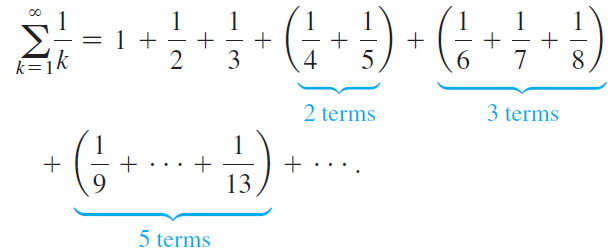
With the Fibonacci sequence in mind, show that

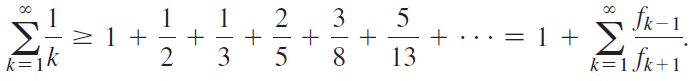
d. Use part (b) to conclude that the harmonic series diverges.

Sfn+1 fn fn+1 1 + V5 - lim fn 1.618. ||