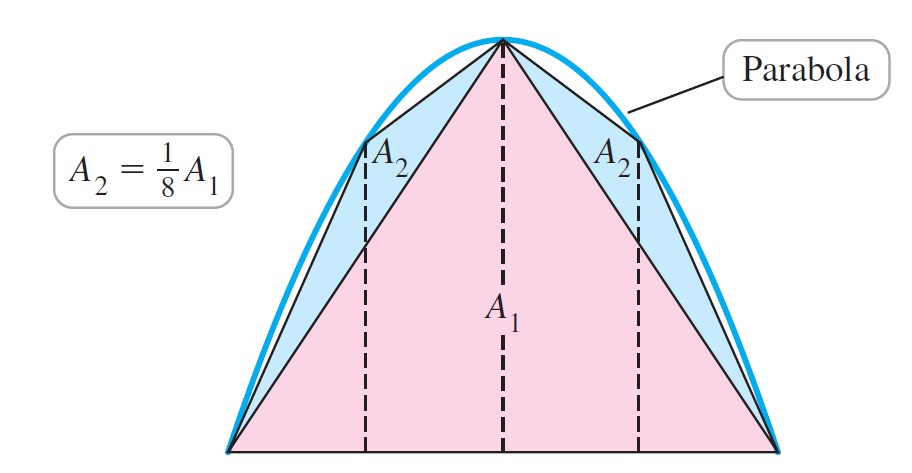
The Greeks solved several calculus problems almost 2000 years before the discovery of calculus. One example is Archimedes’ calculation of the area of the region R bounded by a segment of a parabola, which he did using the “method of exhaustion.” As shown in the figure, the idea was to fill R with an infinite sequence of triangles. Archimedes began with an isosceles triangle inscribed in the parabola, with area A₁, and proceeded in stages, with the number of new triangles doubling at each stage. He was able to show (the key to the solution) that at each stage, the area of a new triangle is 1/8 of the area of a triangle at the previous stage; for example, A₂ = 1/8 A₁, and so forth. Show, as Archimedes did, that the area of R is 4/3 times the area of A₁.

Parabola A2 A, = A, 2.