A company needs to construct a box with an open top that will be used to transport 400yd³ with an open top that will be used to transport of material, in several trips, from one place to another. Two of the sides and bottom of the box can be made of a free, lightweight material, but only 4yd² of the material is available. Because of the nature of the material to be transported, the two ends of the box must be made from a heavyweight material that costs $20 per yd². Each trip costs 10 cents.

a. Let x, y, and z denote the length, width, and height of the box, respectively. If we want to use all of the free material, show that the total cost in dollars is given by the function

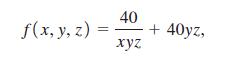
subject to the constraint 2xz + xy = 4.

b. Use the Solver feature on a spreadsheet to find the dimensions of the box that minimize the transportation cost, subject to the constraint.

f(x,y,z) = 40 xyz + 40yz,