Each of Exercises 81 through 85 involves either the chain rule for partial derivatives or the incremental approximation formula for functions of two variables.

Suppose y = h(x) is a differentiable function of x and that F(x, y) = C for some constant C. Use the chain rule (with x taking the role of t) to show that

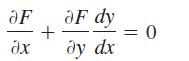
Conclude that the slope at each point (x, y) on the level curve F(x, y) = C is given by

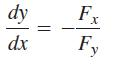
F x + JF dy dy dx = 0