Exercises 36 through 39 require the extreme value property.

In this exercise, you are asked to re-examine Example 7.3.4 as an optimization problem over a closed, bounded region.

a. In Example 7.3.4, explain why the variables x and y must satisfy

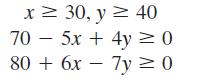
Show that the set of all points (x, y) that satisfy these inequalities is a triangular region, and find its vertices.

b. Solve Example 7.3.4 by finding the largest value of the profit function

over the triangular region found in part (a). Does this change the solution provided? For what values of x and y is the smallest profit obtained?

Data from Exercises 7.3.4.

Jamaal manages a grocery store that carries two brands of cat food, a local brand obtained at the cost of 30 cents per can and a well-known national brand obtained for 40 cents per can. He estimates that if the local brand is sold for x cents per can and the national brand for y cents per can, then approximately 70 − 5x + 4y cans of the local brand and 80 + 6x − 7y of the national brand will be sold each day. How should Jamaal price each brand to maximize total daily profit from the sale of cat food? (Assume that the largest daily profit occurs at a relative maximum.)

x 30, y > = 70 80+ 40 0 = 6x7y 0 5x + 4y