In Exercise 60, Section 2.3, you were given a function to model the production of blood cells. Such models are useful in the study of leukemia and other so-called dynamical diseases in which certain physiological systems begin to behave erratically. An alternative model* for blood cell production developed by A. Lasota involves the exponential production function 

where A, s, and r are positive constants and x is the number of granulocytes (a type of white blood cell) present.

a. Find the blood cell level x that maximizes the production function p(x). How do you know the optimum level is a maximum?

b. If s > 1, show that the graph of p(x) has two inflection points. Sketch the graph. Give a physical interpretation of the inflection points.

c. Sketch the graph of p(x) in the case where 0 ≤ s ≤ 1. What is different in this case?

Data from Exercises 60 section 2.3

A biological model^† measures the production of a certain type of white blood cell (granulocytes) by the function

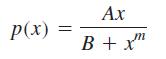
where A and B are positive constants, the exponent m is positive, and x is the number of cells present.

P(x) = Ax'e-sx/r