In Exercise, use the ideas from Exercise 67 to find the derivative of each  unction.

h(x) = (x² + 1)^5x

Data from Exercise 67

Let h(x) = u(x)^v(x).
Using the fact that 

use the chain rule, the product rule, and the formula for the derivative of ln x to show that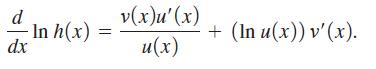

Use the result from part (a) and the fact that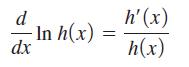

to show that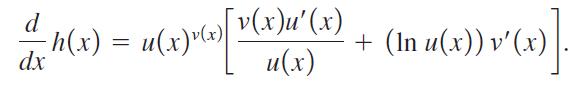

The idea of taking the logarithm of a function before differentiating is known as logarithmic differentiation.

In [u(x)(x)] = v(x) In u(x),