Let g(t) = t 4 and define (x) = 1 0 e x2 dx = 1.46265 and 2 0 e x2 dx =

Let g(t) = t⁴ and define ƒ(x) = ∫¹₀e^x2 dx = 1.46265 and  ∫²₀e^x2 dx = 16.45263. Use this information to find

(a)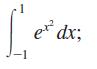

(b) Verify that ƒ′(1) = g(x). The fact that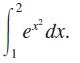

is true for all continuous functions g is an alternative version of the Fundamental Theorem of Calculus.

(c) Let us verify the result in part (b) for a function whose antiderivative cannot be found. Let g(t) = e^t2 and let c = 0. Use the integration feature on a graphing calculator to find ƒ(x) for x = 1 and x = 1.01. Then use the definition of the derivative with h = 0.01 to approximate ƒ′(1), and compare it with g(1).

-1 e dx;