Suppose that 0 < N < y 0 . Let b = (y 0 - N)/y 0 and let See the figure. Show the following.

Suppose that 0 0 . Let b = (y₀ - N)/y₀ and let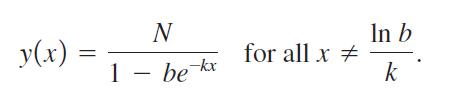

See the figure. Show the following.

(a) 0

(b) The lines y = 0 and y = N are horizontal asymptotes of the graph.

(c) The line x = (ln b)/k is a vertical asymptote of the graph.

(d) y(x) is decreasing on ((ln b)/k, ∞) and on (-∞, (ln b)/k).

(e) y(x) is concave upward on ((ln b)/k, ∞) and concave downward on (-∞, (ln b)/k).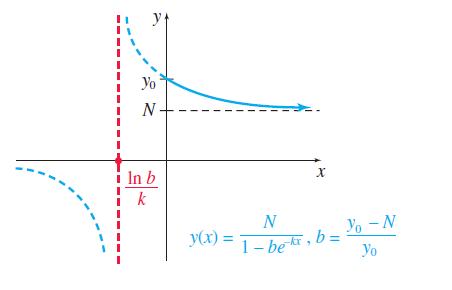

y(x) = N 1-be-kx for all x # In b k