Question: The ancient Babylonians (circa 1700 B.C.) approximated N by applying the formula Show that this formula can be derived from the formula for Newtons method

The ancient Babylonians (circa 1700 B.C.) approximated √N by applying the formula

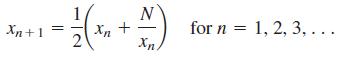
Xn+1 = 1/(x N Xxn + Xn. for n = 1, 2,

Show that this formula can be derived from the formula for Newton’s method in Exercise 33, and then use it to estimate √1,265. Repeat the formula until two consecutive approximations agree to four decimal places. Use your calculator to check your result.

Data from Exercises 33

Show that when Newton’s method is applied repeatedly, the nth approximation is obtained from the (n − 1)st approximation by the formula

3, ...

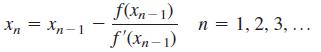
Xn+1 = 1/(x N Xxn + Xn. for n = 1, 2, 3, ...

Step by Step Solution

★★★★★

3.53 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Suppose N is a fixed number ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus With Applications Questions!

Compute u + v and u 2v. U= [-2], x= [1 V= -3 3 ]

Let R be the set of points with 1 x 2 and 0 y 1 and 8(x, y) = x. Find the inertia when R is rotated around the line x = y. (The distance between (a, b) and the line x = y is d = |a-bl/2). The...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

In Problem we introduced the Cobb-Douglas production function of the form q = Ka Lb. The cost function that can be derived from this production function is: TC = Bq1/(a+b)va/(a+b)wb/(a+b), where B is...

Using "On the Spectrum of Hydrogen" by Niels Bohr -What is the main idea of the Author's argument? What is the main essence of the piece? -What ways does the author use to propose and support their...

Study Guide Healthcare Statistics By Jacqueline K. Wilson, RHIA About the Author Jacqueline K. Wilson is a Registered Health Information Administrator (RHIA) who has more than ten years of experience...

I am working on a homework problem and am stumped on part B. Kim hotels is interested in developing a new hotel in seoul. The company estimates that the hotel would require an initial investment of...

More than 4,000 years ago, the ancient Babylonians used a numerical system that is well known for being the first positional numerical system. In such a system, a non-negative integer is represented...

Exercise 3 : Square Root, Babylonian Style The ancient Babylonians produced a remarkably efficient process to compute the square root of any number n . The method is referred to as a guess and check...

This is a C++ problem. Please give full explanation and code in details. Thanks. The ancient Babylonians produced a remarkably efficient process to compute the square root of any number n. The method...

Identify what way of counting we use today that was used by the Ancient Babylonians. Group of answer choices base 1 2 base 1 0 base 6 0 We do not use any of the same systems.

5) The following are transactions for the city of Springfield. a. Borrowed $20,000 by issuing a three-month, 5% note.

Given rectangular grid and the 3 types of pieces shown below, the object of Stretch is to place piece in the grid so that they from a connected path from the left side to the right side. ? A piece...

most sales in property taxes in the United States employ a a consumption rate structure b progressive rate structure C regressive rate structure proportional reach structure

1.2 Identify the four goals of psychological research.

Integration by parts should be used to evaluate Determine whether each of the following statements is true or false, and explain why. Jo 10x xel dx.

The total money flow is found by taking the derivative of the function giving the rate of money flow. Determine whether each statement is true or false, and explain why.

A right circular cone is an example of a volume of revolution. Determine whether each statement is true or false, and explain why.

Valber Company is considering eliminating its Phone division. The company allocates fixed costs based on salos. If the Phone division is dropped, all of its variable costs are avoidable, and $160,000...

Problem 3 (100 points) Parky Co. manufactured 100,000 units of Wood Tables in 20X9 and reported the following costs: Direct labor Direct materials, 1/1/X9 Direct material purchases Direct materials,...

app, but nat both. Consider the following cath flows of the two mutually exclualve projects for Nintendo. Awsume the discount rate for Nintende is 10\%. Given the same Gash flow, compite the iRR of...