The general probability density function has the form where and are constants, with >
Question:
The general probability density function has the form
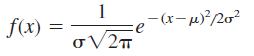
where μ and σ are constants, with σ > 0.
a. Show that f (x) has an absolute maximum at x =μ and inflection points at x = μ + σ and x =μ − σ.
b. Show that f(μ + c) = f(μ − c) for every number
c. What does this tell you about the graph of f(x)?
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a Noting that 2 and are all constants and that So there are infle...View the full answer
Answered By
Charles mwangi
I am a postgraduate in chemistry (Industrial chemistry with management),with writing experience for more than 3 years.I have specialized in content development,questions,term papers and assignments.Majoring in chemistry,information science,management,human resource management,accounting,business law,marketing,psychology,excl expert ,education and engineering.I have tutored in other different platforms where my DNA includes three key aspects i.e,quality papers,timely and free from any academic malpractices.I frequently engage clients in each and every step to ensure quality service delivery.This is to ensure sustainability of the tutoring aspects as well as the credibility of the platform.
2+ Reviews
10+ Question Solved
Related Book For 
Calculus For Business, Economics And The Social And Life Sciences
ISBN: 9780073532387
11th Brief Edition
Authors: Laurence Hoffmann, Gerald Bradley, David Sobecki, Michael Price
Question Posted:
