The logistic equation introduced in Section 1,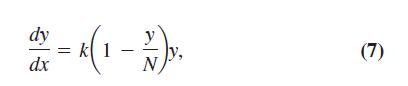

can be written as

where c and p are positive constants. Although this is a nonlinear differential equation, it can be reduced to a linear equation by a suitable substitution for the variable y.
(a) Letting y = 1/z and dy/dx = (-1/z²)dz/dx, rewrite Equation (8) in terms of z. Solve for z and then for y.
(b) Let z(0) = 1/y₀ in part (a) and find a particular solution for y.
(c) Find the limit of y as x→ ∞. This is the saturation level of the population.

dy dx = k 1 - 2)y, (7)