Question: Given three distinct points on a circle (x 1 , y 1 ), (x 2 , y 2 ), and (x 3 , y 3

Given three distinct points on a circle (x1, y1), (x2, y2), and (x3, y3), we can find the equation of the circle by using the following 4 x 4 determinant equation.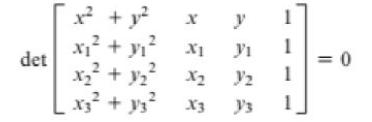det x + + y +y x + 1/ 2 X3 +


Find the equation of the circle through the given points.y3 X1 y 1 X2 2 1 X3 Y3 1 0 =

det x + + y +y x + 1/ 2 X3 + y3 X1 y 1 X2 2 1 X3 Y3 1 0 =

Step by Step Solution

★★★★★

3.44 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

y 1 1 1 1 2 1 1 8 2 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related College Algebra Graphs And Models Questions!

Q:

Find the equation of the circle x2 + y2 + Dx + Ey + F = 0 that passes through the points. To verify your result, use a graphing utility to plot the points and graph the circle. (2, 1) 1 2 3 4 (5, 2)...

Q:

A department store conducted an experiment to investigate the effects of advertising expenditures on the weekly sales for its men's wear, children's wear, and women's wear departments. Five weeks for...

Q:

The idea is to get an equation from the vanishing of the determinant of a homogeneous linear system as the condition for a nontrivial solution in Cramers theorem. We explain the trick for obtaining...

Q:

Given three distinct points on a circle (x 1 , y 1 ), (x 2 , y 2 ), and (x 3 , y 3 ), we can find the equation of the circle by using the following 4 x 4 determinant equation. Find the equation of...

Q:

Given three distinct points on a circle (x 1 , y 1 ), (x 2 , y 2 ), and (x 3 , y 3 ), we can find the equation of the circle by using the following 4 x 4 determinant equation. Find the equation of...

Q:

Given three distinct points on a circle (x 1 , y 1 ), (x 2 , y 2 ), and (x 3 , y 3 ), we can find the equation of the circle by using the following 4 x 4 determinant equation. Find the equation of...

Q:

solve this question Suppose that we want to find a polynomial function g(t) = 1 + rat + rat + rat with parameters 21, 72. c3, 24 such that the following conditions are satisfied. . Given three...

Q:

solve this question Suppose that we want to find a polynomial function g(t) = 1 + rat + rat + rat with parameters 21, 72. c3, 24 such that the following conditions are satisfied. . Given three...

Q:

Determine whether given points are on the graph of the given circle (x - 1) ^ 2 + (y + 1) ^ 2 = 49 Enter Yes or No for your answers: Is (1, 6) on the graph? Is(0, - 1) on the graph? Is (0, 0) on the...

Q:

Determine whether given points are on the graph of the given circle (x - 1) ^ 2 + (y + 1) ^ 2 = 49 Enter Yes or No for your answers: Is (1, 6) on the graph? Is(0, - 1) on the graph? Is (0, 0) on the...

Q:

Bamfram plc is a well established manufacturer of a specialized product, a Wallop, which has the following specifications for production: The sales manager informs Mr. Jones that despite adverse...

Q:

Two forces are applied as shown to a hook support. Using trigonometry and knowing that the magnitude of P is 14 lb, determine (a) The required angle α if the resultant R of the two forces...

Q:

If a firm is hiring labor in the perfectly competitive labor market, the wage and employment will be (A) $4 and 0. (B) $5 and 10. (C) $6 and 20. (D) $7 and 30. (E) $8 and 40.

Q:

25. An ecologist wishes to mark off a circular sampling region having radius 10 m. However, the radius of the resulting region is actually a random variable R with pdf What is the expected area of...

Q:

In an acid-base titration, a base or acid is gradually added to the other until they have completely neutralized each other. Because acids and bases are usually colorless (as are the water and salt...

Q:

Six tissues are extracted from an ivy plant infested by spider mites. The plant in infested in 20% of its area. Each tissue is chosen from a randomly selected area on the ivy plant. (a) What is the...

Q:

A player of a video game is confronted with a series of four opponents and an 80% probability of defeating each opponent. Assume that the results from opponents are independent (and that when the...

Q:

Clear Limited has purchased a new machine and is unclear how much to include in the Cost a/c. You are provided with the following information in relation to expenditure on the machine during the...

Q:

Read the Accounting for Software Development Activities Case Study (link below). After reading the case study, answer the questions provided. While Ms. Larson is confident with regard to the U.S....

Q:

Do ratio tell the whole story