Question: Consider the following proof that log 2 16 does not exist. The logarithm of a negative number is not defined, so the final step cannot

Consider the following “proof” that log2 16 does not exist.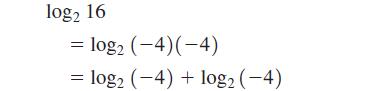log 16 log (-4) (-4) = log (-4) + log (-4)


The logarithm of a negative number is not defined, so the final step cannot be evaluated. Thus log2 16 does not exist.

log 16 log (-4) (-4) = log (-4) + log (-4)

Step by Step Solution

★★★★★

3.41 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The proof presented is incorrect It is based on a misunderstanding of the properties of l... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related College Algebra Questions!

Q:

Please help with the discusin questions ! I give thumbs up Case #1: Hailing a New Era: Haier in Japan As one of the most valuable brands in China, Haier designs,manufactures, and sells various home...

Q:

Describe the error in the following proof that 0 * 1 * is not a regular language. (An error must exist because 0 * 1 * is regular.) The proof is by contradiction. Assume that 0 * 1 * is regular. Let...

Q:

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Q:

1. Read the articleSix Impossible Things Before Breakfast. Is the Efficient Market Hypothesis (EMH) the correct theory relative well functioning financial markets? If not why not? 2.Read the...

Q:

UNIT 5 QZ, Q-20 UNIT 5 / UNIT 8 QUESTIONS KEEP ANSWERS SEPARATE BY UNITS UNIT II STUDY GUIDE Consumer Mathematics Reading Assignment See information below. Key Terms 1. Add-on interest method 2....

Q:

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Q:

Defense Cross Examination of Corey Hyde 1. D: \"Mr. Hyde, is it true when you originally acquired your position as Avery Bancroft's assistant at the Black Bear Casino, you were not thrilled at the...

Q:

Fundamentals of Project Management Fourth Edition by Reza Torkzadeh FUNDAMENTALS OF PROJECT MANAGEMENT Reza Torkzadeh Copyright 2012-2013 by Reza Torkzadeh. All rights reserved. No part of this...

Q:

Math 1330 Precalculus Electronic Homework (EHW 2) Algebra Review You have 2 electronic homework assignments over Algebra Review (EHW 1 and EHW 2); be careful about choosing the correct EMCF title...

Q:

s sf Define the terms opaque type and concrete type. [5 marks] The following is a shortened version of one of the definition modules described in the Modula-2 user manual: Provide a suitable...

Q:

what's the structure model of y (t), and also determine the correlation and expected value of y (t) y (t) A (Ay(t-3) + e(t 2)) + Ae(t 1) + e(t)

Q:

Find the periodic payment which will amount to a sum of $8000 if an interest rate 7% is compounded annually at the end of 14 consecutive years. The periodic payment is $ (Round to the nearest cent.)

Q:

Please show ALL of your work. show all calculations. thanks

Q:

Why did Elaine finally decide to seek treatment?

Q:

A buyer decides to stock 8 different posters. How many ways can she select these 8 if there are 20 from which to choose?

Q:

Anderson Research Company decides to test-market a product in 6 areas. How many different ways can 3 areas be selected in a certain order for the first test?

Q:

How many different ways can a government researcher select 5 nuclear power plants from 9 nuclear power plants in Pennsylvania?

Q:

Under the alternative depreciation system (ADS), the half-year convention must be used for personality. T/F

Q:

At June 1, 2011, Larry Levine Company reported Accounts Payable of $10,000. During the month, the company made purchases on account of $34,000 and payments on account of $20,000. At June 30, 2011,...

Q:

Berry Company sold goods with a total selling price of $804,830 during the year. It purchased goods for $400,800 and had beginning inventory of $74,860. A count of its ending inventory determined...