Question: Solve the problem. Consider the figure, which is a square divided into two squares and two rectangles. (a) The length of each side of the

Solve the problem.

Consider the figure, which is a square divided into two squares and two rectangles.

(a) The length of each side of the largest square is x + y. Use the formula for the area of a square to write the area of the largest square as a power.

(b) Use the formulas for the area of a square and the area of a rectangle to write the area of the largest square as a trinomial that represents the sum of the areas of the four figures that make it up.

(d) What special product formula from this section does this exercise reinforce geometrically?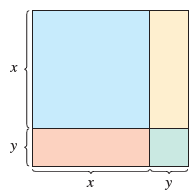 х х

Step by Step Solution

★★★★★

3.35 Rating (188 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The area of the largest square is s x y b The areas of the two squares ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related College Algebra Questions!

Solve the problem. Use the figure to geometrically support the distributive property. Write a short paragraph explaining this process.

The graph shows the number of farms in the United States for selected years since 1950. We can use the formula Number of farms = 0.001259x 2 - 5.039x + 5044 to get a good approximation of the number...

The special products can be used to perform selected multiplications. On the left, we use (x + y)(x - y) = x 2 - y 2 . On the right, (x - y) 2 = x 2 - 2xy + y 2 . Use special products to evaluate...

I really need help with this python assignment please indent & double check This assignment has two parts and isn't nearly as formidable as it looks (although you shouldn't wait until the last minute...

A gray square with an area of 36 cm' and a black square with an area of 25 cm? are superimposed, as shown beside. What is the perimeter of the overlapping region, represented by the white...

Instructions: Complete the following exercises. Create a folder of your own and use it to store your solutions. When you have completed the assignments, compress (zip) the folder and upload the...

In 1999, Linda McGuire, manager of purchasing and customs at Amway of Canada's London, Ontario headquarters, faced a complicated decision regarding the purchase of new photocopiers. The company's six...

WIGULUSLUUPLIUI You will write a program using functions that performs the following tasks. These tasks are explained in more detail later in this document (1) For a user specified number of...

Question: The work below is not the work of a tutor. I am submitting these problems for the first time. The work is my own. It is just me, the problems, and my text book. The work that I have...

You will write a program using functions that performs the following tasks. These tasks are explained in more detail later in this document (1) For a user specified number of iterations, determine an...

After reading After the Bell Curve, do you believe that IQ is solely influenced by genetics? What advice would you offer to parents/caregivers/and educators in order to maximize IQ?

AIM: Write C program for sorting using a pointer.

Marcellus invests $ 5 0 0 today to save for a holiday. He deposits the $ 5 0 0 at Westpac at 6 % p . a . compounded monthly for 2 years. What is the annual effective interest rate ( as a % with 2...

1. What are the objectives of short-term financial planning?

In Exercises 1326, use vertices and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. 2 X 144 81 = 1

In Exercises 1218, graph each equation. (x + 1) 2 + (y - 1) 2 = 4

In Exercises 118, graph each ellipse and locate the foci. 4x 2 + 25y 2 = 100

In a survey of 1,100 organizations, 840 responded that "the need for collaboration among an increasing number of locations" is a business driver that led them to implement cloud solutions. Construct...

Math134 F21 Marques Wood Test: Exam(1) Question 13 This Test: 80 pts possible A certain standardized test's math scores have a bell-shaped distribution with a mean of 520 and a standard deviation of...

Sloan Transmissions, Inc., has the following estimates for its new gear assembly project: price = $1,300 per unit; variable costs = $260 per unit; fixed costs = $4.8 million, quantity = 72,000 units....