A process is simulated by the second-order passive circuit, shown in Figure P5.52, where the feedback amplifier, controller, and final control element are represented by op-amp circuits.

a. Denoting the input and output as R(s) = V_i (s) and C(s) = V_o(s), with R(s) - C(s) = E(s), and noting that the feedback amplifier has a unity gain, draw a block diagram for this feedback control system, where G_C(s), G_F(s), and G_P(s) are the transfer functions of the controller, final control element, and the process, respectively.

b. Find the value of R_P that makes the circuit representing the process critically damped.

c. Noting that the proportional controller is simply an amplifier, G_C(s) = K_P, find the value of its gain K_P that results in dominant closed-loop poles with a damping ratio, ζ = 0:5, and a settling time, T_s = 4 ms. Verify that the other pole is non dominant. What would be the appropriate value of the controller potentiometer, RF, given that its tolerance is ±10%?

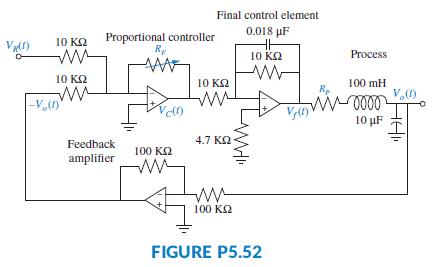
Final control element 0.018 pF 10 K2 Proportional controller 10 KQ Process 10 KQ 10 K2 100 mH V,) Vel) 10 F 4.7 K2 Feedback 100 K2 amplifier 100 K2 FIGURE P5.52